Bài 3 trang 80 SGK Toán 8 Tập 1 Chân trời sáng tạo

Bài 3 trang 80 SGK Toán 8 Tập 1 Chân trời sáng tạo: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.

a) Chứng minh rằng tứ giác EBFD là hình bình hành.

b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.

Giải bài 3 trang 80 SGK Toán 8 Tập 1 Chân trời sáng tạo:

• Ta có hình vẽ minh hoạ như sau: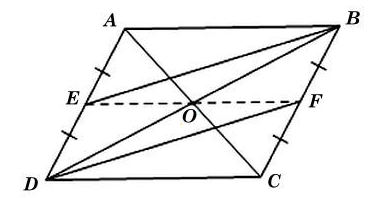

a) ABCD là hình bình hành nên AD = BC và AD // BC.

Mà E là trung điểm của AD nên AE = ED;

F là trung điểm của BC nên BF = FC.

⇒ DE = BF.

• Xét tứ giác EBFD có:

DE // BF (do AD // BC) và DE = BF

⇒ EBFD là hình bình hành (dấu hiệu nhận biết).

b) Ta có O là giao điểm của hai đường chéo của hình bình hành ABCD nên O là trung điểm của BD.

Do EBFD là hình bình hành nên hai đường chéo BD và EF cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD

Nên O là trung điểm của EF.

⇒ Ba điểm E, O, F thẳng hàng.