Số thực là gì, gồm những số nào, cho ví dụ? Số đối là gì? Số đối của số thực và giá trị tuyệt đối của một số thực Toán 7 bài 2 CTST

Bài này giúp các em hiểu rõ về Số thực, tập hợp các số thực. Thứ tự trong tập hợp các số thực. Trục số thực, số đối của một số thực và giá trị tuyệt đối của một số thực.

1. Số thực và tập hợp các số thực

– Ta gọi chung số hữu tỉ và số vô tỉ là số thực.

– Tập hợp số thực được kí hiệu ℝ.

Cách viết x ∈ ℝ cho ta biết x là một số thực.

– Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau:

+ Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu số đó là số hữu tỉ.

+ Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.

* Ví dụ: Ta có các số: 5; -2; 0,25; ; ; ; ; ,... là các số thực

Ta viết 5 ∈ ℝ ; –2 ∈ ℝ ; 0,25 ∈ ℝ ; ;; ; ; ;...

> Chú ý: Trong các tập hợp đã học, tập hợp số thực là "rộng lớn" nhất bao gồm tất cả các số tự nhiên, số nguyên, số hữu tỉ và cả số vô tỉ.

– Trong tập hợp các số thực, ta cũng có các phép tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.

2. Thứ tự trong tập hợp các số thực

– Các số thập phân hữu hạn hoặc vô hạn đều có thể so sánh tương tự như so sánh hai số thập phân hữu hạn, đó là so sánh phần số nguyên, rồi đến phần thập phân thứ nhất, phần thập phân thứ hai, …

– Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng.

Do vậy: Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.

> Chú ý: Với hai số thực dương a và b, ta có: Nếu  thì 

* Ví dụ: So sánh hai số thực:

a) 3,(56) và 3,566;

b) √3 và 1,733;

c) –1,021 và –1,022;

d) √8 và 3.

* Lời giải

a) Số 3,(56) = 3,565656… < 3,566 (do phần thập phân thứ ba của hai số ta thấy 5 < 6).

Vậy 3,(56) < 3,566.

b) Ta có: √3= 1,73205... < 1,733 (do phần thập phân thứ ba của hai số ta thấy 2 < 3).

Vậy √3 < 1,733.

c) Ta có: 1,021 < 1,022 (do phần thập phân thứ ba của hai số ta thấy 1 < 2)

Suy ra: –1,024 > –1,025.

Vậy –1,024 > –1,025.

d) Do 8 < 9 nên ta có √8 < √9, tức là √8 < 3 (vì √9= 3).

Vậy √8 < 3.

3. Trục số thực

Ta đã biết một hình vuông có cạnh bằng 1 có độ dài đường chéo là √2.

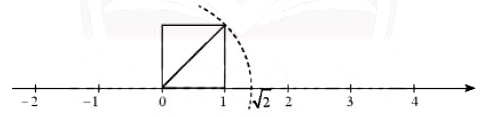
– Trên trục số ta biểu diễn được số vô tỉ √2. Vì vậy, không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ, nghĩa là các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

Người ta chứng minh được rằng:

+ Mỗi số thực được biểu diễn bởi một điểm trên trục số

+ Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

Vì vậy, ta gọi trục số là trục số thực.

> Chú ý:

– Điểm biểu diễn số thực x trên trục số được gọi là điểm x. 

– Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

* Ví dụ: Ta có: √2 = 1,414213562...< 1,5.

Vậy điểm √2 nằm bên trái điểm 1,5 trên trục số nằm ngang.

4. Số đối của một số thực

– Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số thực x kí hiệu là –x.

– Ta có x + (– x) = 0.

* Ví dụ: Số đối của số -4,5 là 4,5, số đối của 4,5 là -4,5.

Số đối của  là  số đối của  là 

5. Giá trị tuyệt đối của một số thực

Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.

Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.

Nhận xét: Ta có: 

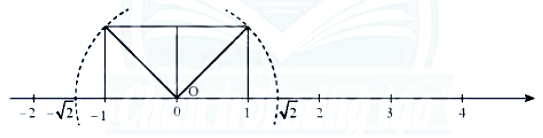Khoảng cách từ điểm đến điểm 0 là  nên

Như vậy ta thấy:

+ Hai số đối nhau thì có giá trị tuyệt đối bằng nhau

+ Giá trị tuyệt đối của 0 là 0

+ Giá trị tuyệt đối của một số dương là chính nó

+ Giá trị tuyệt đối của một số âm là số đối của nó

+ Giá trị tuyệt đối của một số thực luôn không âm.

* Ví dụ: Ta có |3,5| = 3,5

Lại có: |-3,5| = 3,5

Nên |-3,5| = |3,5|

> Chú ý: Giả sử 2 điểm A và B lần lượt biểu diễn 2 số thực a và b khác nhau trên trục số. Khi đó, độ dài của đoạn thẳng AB là |a – b|