Đa thức một biến là gì? Cách sắp xếp, tính giá trị đa thức một biến và Bài tập - Toán 7 tập 2 bài 7
Khái niệm về đa thức các em đã được làm quen, với đa thức chỉ chứ một loại biến như biến x, hoặc chỉ chứa biến y thì người ta gọi là đa thức một biến.
Cụ thể đa thức một biến là gì? cách sắp xếp đa thức một biến như thế nào? chúng ta sẽ cùng tìm hiểu qua nội dung bài viết này.
1. Đa thức một biến là gì?
- Đa thức một biến là tổng của những đơn thức của cùng một biến.
* Ví dụ: Các đa thức sau là đa thức một biến:
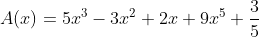 là đa thức của biến x;
là đa thức của biến x;
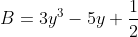 là đa thức của biến y;
là đa thức của biến y;
> Lưu ý: Một số cũng được coi là đa thức một biến.
2. Bậc của đa thức một biến
- Bậc của đa thức một biến khác đa thức không (đã thu gọn) là số mũ lớn nhất của biến có trong đa thức đó.
* Ví dụ: Tìm bậc của đa thức A(x) và B(y) sau:
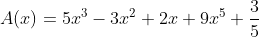
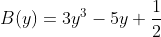
* Lời giải:
- Ta có: 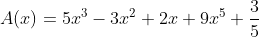
Đa thức A(x) có 5 hạng tử là: 9x5 có bậc 5; 5x3 có bậc 3; -3x2 có bậc 2; 2x có bậc 1; 3/5 có bậc 0;
Mà bậc của đa thức là bậc của hạng tử có bậc cao nhất (9x5 là 5) nên bậc của đa thức A(x) là 5.
- Ta có : 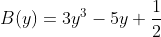
Đa thức B(y) có 3 hạng tử là: 3y3 có bậc 3; – 3y có bậc 1; 1/2 có bậc 0;
Mà bậc của đa thức là bậc của hạng tử có bậc cao nhất (3y3 là 3) nên bậc của đa thức B(y) là 3.
> Lưu ý: Trước khi tìm bậc của đa thức một biến chúng ta cần sắp xếp và rút gọn đa thức để tránh nhầm lẫn.
3. Cách sắp xếp đa thức một biến
- Nhằm thuận tiện trong tính toán đối với các đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến. (Trong các tính toán, chúng ta thường sắp xếp theo lũy thừa giảm dần)
* Ví dụ: Đối với đa thức: P(x) = 6x + 3 - 6x2 + x3 + 2x4
Khi sắp xếp các hạng tử của nó theo lũy thừa giảm của biến ta được:
P(x) = 2x4 + x3 - 6x2 + 6x + 3
và theo lũy thừa tăng của biến, ta được:
P(x) = 3 + 6x - 6x2 + x3 + 2x4
> Lưu ý: Để sắp xếp các hạng tử của đa thức, trước tiên ta phải thu gọn đa thức đó.
4. Hệ số và cach tính giá trị của đa thức một biến
• Hệ số của đa thức
- Hệ số cao nhất là hệ số của số hạng có bậc cao nhất.
- Hệ số tự do là số hạng không chứa biến.
* Ví dụ: Xét đa thức: P(x) = 6x5 + 7x3 - 3x + 1/2
Ta nói 6 là hệ số của lũy thừa bậc 5 (hệ số cao nhất của số hạng cao nhất); 7 là hệ số của lũy thừa bậc 3; -3 là hệ số của lũy thừa bậc 1; 1/2 là hệ số của lũy thừa bậc 0 (hệ số tự do).
• Cách tính giá trị của đa thức một biến.
- Giá trị của đa thức f(x) = a được kí hiệu là f(a) có được bằng cách thay x = a vào đa thức f(x) rồi thu gọn lại.
* Ví dụ: Tính giá trị của đa thức P(x) = 6x5 + 7x3 - 3x + 1/2 tại x = 1;
* Lời giải:
- Ta tính P(2) = 6.(1)5 + 7.(1)3 - 3.1 + 1/2 = 6 + 7 - 3 + 1/2 = 21/2.
5. Bài tập về đa thức một biến
* Bài 39 trang 43 SGK Toán 7 tập 2: Cho đa thức: P(x) = 2 + 5x2 – 3x3 + 4x2 – 2x – x3 + 6x5
a) Thu gọn và sắp xếp các hạng tử của P(x) theo lũy thừa giảm của biến.
b) Viết các hệ số khác 0 của đa thức P(x).
* Lời giải:
a) P(x) = 2 + 5x2 – 3x3 + 4x2 –2x – x3 + 6x5
P(x) = 2 + (5x2+ 4x2) + (– 3x3– x3) – 2x + 6x5
P(x) = 2 + 9x2 – 4x3– 2x + 6x5
Sắp xếp các hạng tử của P(x) theo lũy thừa giảm của biến, ta có
P(x) = 6x5 – 4x3 + 9x2 – 2x + 2
b) Hệ số của lũy thừa bậc 5 là 6
Hệ số của lũy thừa bậc 3 là – 4
Hệ số của lũy thừa bậc 2 là 9
Hệ số của lũy thừa bậc 1 là – 2
Hệ số của lũy thừa bậc 0 là 2
* Bài 40 trang 43 SGK Toán 7 tập 2: Cho đa thức Q(x) = x2 + 2x4 + 4x3 – 5x6 + 3x2 – 4x – 1
a) Sắp xếp các hạng tử của Q(x) theo lũy thừa giảm của biến.
b) Chỉ ra các hệ số khác 0 của Q(x).
* Lời giải:
a) Q(x) = x2 + 2x4 + 4x3 – 5x6 + 3x2 – 4x –1
Q(x) = (x2+ 3x2) + 2x4 + 4x3 – 5x6– 4x –1
Q(x) = 4x2 + 2x4 + 4x3 – 5x6 – 4x –1
Sắp xếp các hạng tử của Q(x) theo lũy thừa giảm của biến, ta có
Q(x) = – 5x6 + 2x4 + 4x3 + 4x2 – 4x –1
b) Hệ số lũy thừa bậc 6 là – 5
Hệ số của lũy thừa bậc 4 là 2
Hệ số của lũy thừa bậc 3 là 4
Hệ số của lũy thừa bậc 2 là 4
Hệ số của lũy thừa bậc 1 là –4
Hệ số của lũy thừa bậc 0 là –1.
* Bài 41 trang 43 SGK Toán 7 tập 2: Viết một đa thức một biến có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là -1.
* Lời giải:
Đa thức bậc nhất thỏa mãn các điều kiện trên: 5x - 1
Đa thức bậc hai thỏa mãn các điều kiện trên: 5x2 - 1
Đa thức bậc ba thỏa mãn các điều kiện trên: 5x3 - 1
Đa thức bậc bốn thỏa mãn các điều kiện trên: 5x4 - 1
. . .
Tổng quát: Đa thức bậc n (n là số tự nhiên): 5xn - 1
* Bài 42 trang 43 SGK Toán 7 tập 2: Tính giá trị của đa thức P(x) = x2 – 6x + 9 tại x = 3 và tại x = -3.
* Lời giải:
- Thay x = 3 vào biểu thức P(x) ta được: P(3) = 32 – 6.3 + 9 = 9 - 18 + 9 = 0
Vậy P(3) = 0.
- Thay x = – 3 vào biểu thức P(x) ta được: P(– 3) = (– 3)2 – 6.(–3) + 9 = 9 + 18 + 9 = 36
Vậy P(-3) = 36.
* Bài 43 trang 43 SGK Toán 7 tập 2: Trong các số cho ở bên phải mỗi đa thức, số nào là bậc của đa thức đó?
| a) 5x2 – 2x3 + x4 – 3x2 – 5x5 + 1 | –5 5 4 |
| b) 15 – 2x | 15 – 2 1 |
| c) 3x5 + x3 – 3x5 + 1 | 3 5 1 |
| d) –1 | 1 –1 0 |
* Lời giải:
a) 5x2 – 2x3 + x4 – 3x2 – 5x5 + 1 = (5x2 – 3x2) – 2x3 + x4– 5x5 + 1
= 2x2 – 2x3 + x4– 5x5 + 1 = -5x5 + x4 – 2x3 + 2x2 +1.
⇒ Bậc của đa thức là 5.
b) 15 – 2x = -2x1 +15.
⇒ Bậc của đa thức là 1.
c) 3x5 + x3 - 3x5 +1 = (3x5 – 3x5) + x3 +1 = x3 + 1.
⇒ Bậc của đa thức bằng 3.
d) Đa thức -1 có bậc bằng 0.
Tóm lại, với bài viết này các em cần ghi nhớ đa thức một biến là gì? các hệ số của đa thức một biến, cách sắp xếp và tính giá trị của đa thức một biến tại một giá trị của x.
Đánh giá & nhận xét

- Tìm m để đường thẳng tiếp xúc với đường tròn Toán 10 - Hỏi nhanh đáp gọn
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của tam thức bậc 2
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa trị tuyệt đối
- Tìm giá trị nhỏ nhất (gtnn), giá trị lớn nhất (gtln) của biểu thức lớp 9
- Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa dấu căn
- Đơn vị Micro, Nano, Pico? Bảng mẫu đơn vị về ước số và bội số trong SI? Hỏi đáp môn Vật lí
- Hệ đơn vị SI là gì? 7 đơn vị cơ bản của hệ SI? Hỏi nhanh đáp gọn môn Vật lí
- Đặc điểm của Electron lớp ngoài cùng của nguyên tử là gì? Hỏi nhanh Hóa 10
- Cách viết cấu hình Electron nguyên tử lớp 10? Hỏi nhanh Hóa 10
- Quy tắc Hund và Nguyên lý bền vững lớp 10? Hỏi nhanh Hóa 10


































