Cách chứng minh 3 điểm thẳng hàng Toán lớp 7

Bài viết này trình bày chi tiết hướng dẫn cách chứng minh 3 điểm thẳng hàng Toán lớp 7, nhằm giúp các em học sinh ôn tập, vận dụng chứng minh 3 điểm thẳng hàng dễ dàng.

1. Cách chứng minh 3 điểm thẳng hàng lớp 7

• Cách 1: Chứng minh 3 điểm thẳng hàng

Nếu góc ∠ABD + ∠DBC = 180^o thì 3 điểm A; B; C thẳng hàng.

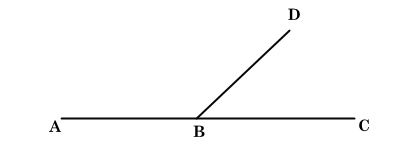
• Cách 2: Chứng minh 3 điểm thẳng hàng

Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.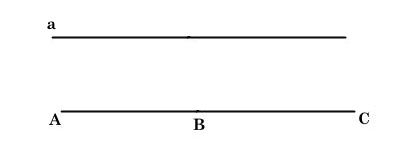

* Cơ sở cách này vận dụng tiền đề Ơ-Clit.

• Cách 3: Chứng minh 3 điểm thẳng hàng

Nếu AB ⊥ a; AC ⊥ a thì 3 điểm A, B, C thẳng hàng.

Hoặc A; B; C cùng thuộc một đường trung trực của một đoạn thẳng.

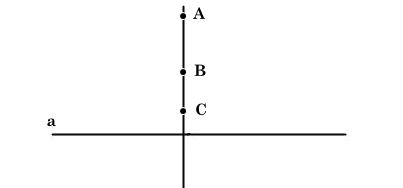
* Cơ sở cách này là: Có một và chỉ một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước.

• Cách 4: Chứng minh 3 điểm thẳng hàng

Nếu tia OA và tia OB là hai tia phân giác của góc xOy thì ba điếm O; A; B thẳng hàng.

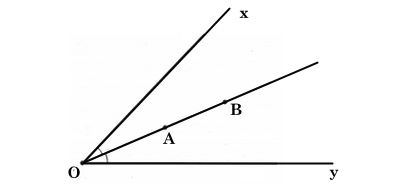
* Cơ sở của cách này là: Mỗi góc khác góc bẹt có một và chỉ một tia phân giác.

* Hoặc: Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox, góc ∠xOA = ∠xOB thì ba điểm O, A, B thẳng hàng.

• Cách 5: Chứng minh 3 điểm thẳng hàng

Nếu K là trung điểm BD, K’ là giao điểm của BD và AC. Nếu K’ là trung điểm BD thì K' ≡ K và A, K, C thẳng hàng.

* Cơ sở của cách này là: Mỗi đoạn thẳng chỉ có duy nhất 1 trung điểm.

2. Chứng minh 3 điểm thẳng hàng qua một số ví dụ

* Ví dụ 1: Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC).Trên tia Cx lấy điểm D sao cho CD = AB. Chứng minh ba điểm B, M, D thẳng hàng.

* Lời giải:

Ta có hình vẽ sau:

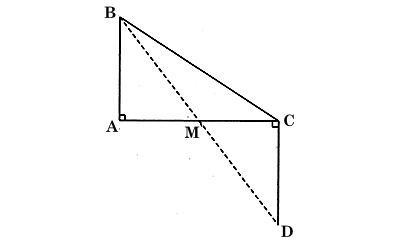Xét tam giác AMB và tam giác CMD, ta có:

AB  = DC (gt)

MA = MC (vì M là trung điểm của AC)

Nên: ΔAMB = ΔCMD (c-g-c)

Mà  (hai gó kề bù)

Nên

Vậy ba điểm B; M; D thẳng hàng.

* Ví dụ 2: Cho hai đoạn thẳng AC và BD cắt nhau tại trung điểm O của mỗi đoạn. Trên tia AB lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho D là trung điểm AN. Chứng minh ba điểm M, C, N thẳng hàng.

* Lời giải:

Ta có hình vẽ sau:

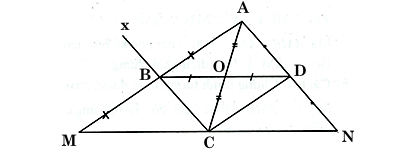° Xét tam giác AOD và COB, ta có:

OA = OC (vì O là trung điểm của AC)

 (hai góc đối đỉnh)

OD = OB (vì O là trung điểm của BD)

Nên ΔAOD = ΔCOB (c-g-c)

 mà hai góc này ở vị trí so le trong

Nên AD // BC

 (hai góc đồng vị)

Xét tam giác DAB và tam giác CBM có:

AD = BC (vì ΔAOD = ΔCOB)

 (chứng mình trên)

AB = BM (vì B là trung điểm của AM)

⇒ ΔDAB = ΔCBM (c-g-c)

 (hai góc ở vị trí đồng vị)

⇒ BD // CM (1)

° Tương tự, Xét tam giác AOB và DOC, ta có:

OA = OC (vì O là trung điểm của AC)

(hai góc đối đỉnh)

OD = OB (vì O là trung điểm của BD)

⇒ ΔAOB = ΔDOC (c-g-c)

 mà hai góc này ở vị trí so le trong

Nên AB // CD

(hai góc đồng vị)

Xét tam giác DAB và tam giác DCN có:

BA = DC (vì ΔAOB = ΔDOC)

(chứng mình trên)

AD = DN (vì D là trung điểm của AN)

⇒ ΔDAB = ΔCDN (c-g-c)

 (hai góc ở vị trí đồng vị)

⇒ BD // CN (2)

Từ (1) và (2) theo tiên đề Ơ-Clit ⇒ ba điểm M, C, N thẳng hàng.