Bài 9.3 trang 82 Toán 8 Kết nối tri thức Tập 2

Bài 9.3 trang 82 Toán 8 Tập 2 Kết nối tri thức:

Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.

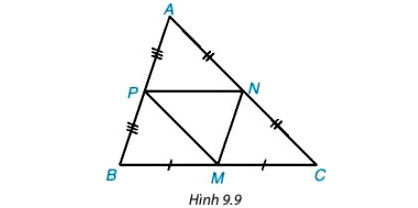
Giải Bài 9.3 trang 82 Toán 8 Tập 2 Kết nối tri thức:

- Vì N, P lần lượt là trung điểm của CA, AB.

⇒ PN là đường trung bình của tam giác ABC nên NP // BC (P ∈ AB, N ∈ AC).

⇒ ΔABC ∽ ΔAPN. 

- Vì M, P lần lượt là trung điểm của BC, AB.

⇒ MP là đường trung bình của tam giác ABC nên MP // AC (P ∈ AB, M ∈ BC)

Suy ra ΔABC ∽ ΔPBM.

- Vì M, N lần lượt là trung điểm của BC, AC.

⇒ MN là đường trung bình của tam giác ABC nên MN // AB (N ∈ AC, M ∈ BC).

⇒ ΔABC ∽ ΔNMC.

- Ta có  (do ΔABC ∽ ΔPBM); 

(do PN // BC); 

  (do cùng bằng góc C);

⇒ ΔAPN ∽ ΔPBM.

- Tương tự ta cũng có ΔNMC ∽ ΔPBM.

- Ta có ΔAPN = ΔMNP (g – c – g) vì 

 (NP // BC và các cặp góc ở vị trí so le trong)

và PN cạnh chung.

⇒ ΔAPN ∽ ΔMNP.

Vậy ta có 5 tam giác APN, PBM, NMC, MNP, ABC đôi một đồng dạng với nhau.