Bài 9.21 trang 76 Toán 7 Kết nối tri thức Tập 2

Bài 9.21 Trang 76 Toán 7 Kết nối tri thức Tập 2: 

Chứng minh rằng:

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Giải bài 9.21 Trang 76 Toán 7 Kết nối tri thức Tập 2: 

Ta có hình vẽ sau:

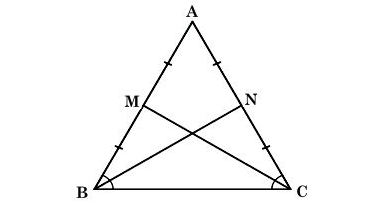
Giả sử tam giác ABC cân tại A có M, N lần lượt là trung điểm của AB và AC.

a) Vì tam giác ABC cân tại A nên AB = AC và 

Do M, N lần lượt là trung điểm của AB và AC nên AB = 2BM, AC = 2CN.

Do đó BM = CN.

Xét ∆MBC và ∆NCB có:

BM = CN (chứng minh trên).

 (chứng minh trên).

BC chung

⇒  ∆MBC = ∆NCB (c - g - c).

Nên CM = BN (2 cạnh tương ứng).

Vậy trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau.

b) Giả sử tam giác ABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G.

G là trọng tâm tam giác ABC nên CG = CM, BG =  BN.

Vì CM = BN nên CG = BG.

Xét ∆BGC có CG = BG nên ∆BGC cân tại G.

Do đó, 

Xét ∆MBC và ∆NCB có:

MC = NB (theo giả thiết).

 (chứng minh trên).

BC chung.

⇒ ∆MBC = ∆NCB (c-g-c).

⇒  (2 góc tương ứng).

Xét ∆ABC có  nên ∆ABC cân tại A.

Vậy nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.