Bài 6 trang 71 Toán 8 Chân trời sáng tạo Tập 2

Bài 6 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF.

b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABC ᔕ ΔMED.

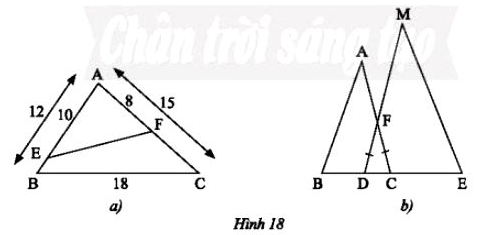
Giải bài 6 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔAFE và ΔABC có:

 chung

Nên ΔAFE ᔕ ΔABC (c.g.c)

Suy ra:  (các cặp cạnh tương ứng).

Khi đó 

Suy ra 

Vậy EF = 12 cm.

b) Xét ΔABC và ΔMED ta có:

 (tam giác FDC cân)

Vậy ΔABC ᔕ ΔMED (c.g.c).