Bài 9.9 trang 65 Toán 7 Kết nối tri thức Tập 2

Bài 9.9 Trang 65 Toán 7 Kết nối tri thức Tập 2: 

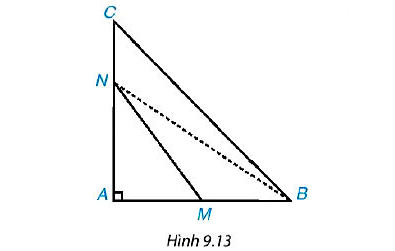
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC.

(M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.

(Gợi ý. So sánh MN với NB, NB với BC).

Giải bài 9.9 Trang 65 Toán 7 Kết nối tri thức Tập 2: 

Ta có  là góc ngoài tại đỉnh M của ∆AMN nên 

.

Vì vậy  là góc tù.

∆NMB có   là góc tù nên  là góc lớn nhất trong ∆NMB.

Vậy cạnh NB là cạnh lớn nhất trong ∆NMB.

Khi đó MN < NB (1).

 là góc ngoài tại đỉnh N của ∆ANB nên 

Vậy có  là góc tù.

Vì  là góc tù nên  là góc lớn nhất trong ∆CNB.

Vậy cạnh BC là cạnh lớn nhất trong ∆CNB.

Khi đó NB < BC (2).

Từ (1) và (2) ta có MN < NB < BC.

Vậy MN < BC.