Bài 4 trang 10 Toán 10 Chân trời sáng tạo Tập 2

Bài 4 trang 10 Toán 10 Chân trời sáng tạo Tập 2: 

Xét dấu của các tam thức bậc hai sau đây:

a) f(x) = 2x² + 4x + 2

b) f(x) = -3x² + 2x + 21

c) f(x) = -2x² + x - 2

d) f(x) = -4x(x + 3) - 9

e) f(x) = (2x + 4)(x - 3)

Giải bài 4 trang 10 Toán 10 Chân trời sáng tạo Tập 2:

Ta có các bước giải như sau:

+ Bước 1: Tính và xác định dấu của biệt thức: Δ = b² - 4ac

+ Bước 2: Xác định nghiệm của f(x) (nếu có) 

+ Bước 3: Xác định dấu của hệ số a

+ Bước 4: Xác định dấu của f(x)

a) f(x) = 2x² + 4x + 2

Có Δ = 4² - 4.2.2 =  0, có nghiệm kép x₁ = x₂ = -1

và a > 0

Ta có bảng xét dấu sau: 

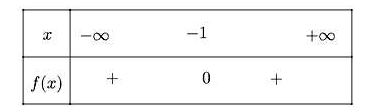
Vậy f(x) > 0 với mọi x ≠ 1

b) f(x) = -3x² + 2x + 21

Có Δ = 256 > 0, có 2 nghiệm phân biệt x₁ = -7/3; x₂ = 3

và a = -3 < 0

Ta có bảng xét dấu sau:

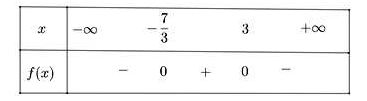
Vậy f(x) > 0 với x ∈ (-7/3;3) và f(x) < 0 với x ∈ (-∞; -7/3) U (3; +∞)

c) f(x) = -2x² + x - 2

Có Δ = -15 < 0, tam thức vô nghiệm

và a = -2 < 0

Ta có bảng xét dấu sau:

Vậy f(x) < 0 với mọi x ∈ R

d) f(x) = -4x(x + 3) - 9 = -4x² - 12x - 9

Có Δ = 0, có nghiệm kép x₁ = x₂ = -3/2

và a = -4 < 0

Ta có bảng xét dấu sau:

Vậy f(x) < 0 với mọi x ≠ -3/2

e) f(x) = (2x + 4)(x - 3) = 2x² - x - 15

Có Δ = 121 > 0, có 2 nghiệm x₁ = -5/; x₂ = 2 > 0

và a = 2 > 0

Ta có bảng xét dấu sau:

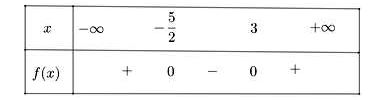
Vậy f(x) < 0 với mọi x ∈ (-5/2; 3) và f(x) > 0 với x ∈ (-∞; -5/3) U (3; +∞)