Bài 12 trang 59 Toán 8 Chân trời sáng tạo Tập 2

Bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho tam giác ABC có BC bằng 30 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (E, M ∈ AB; F, N ∈ AC).

a) Tính độ dài các đoạn thẳng MN và EF.

b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là 10,8 dm².

Giải bài 12 trang 59 Toán 8 Tập 2 Chân trời sáng tạo: 

Ta có hình vẽ sau:

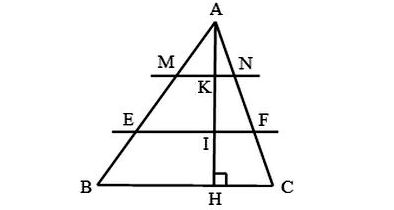
a) Vì MN // BC, theo hệ quả định lí Thalès, ta có:

  (1)

Trong tam giác ABH có MK // BH

 (2)

Từ (1) và (2) suy ra: 

Mà AK = KI = IH nên 

Suy ra:  

Tam giác ABC có EF // BC nên: 

Suy ra:  

Vậy MN = 10 cm và EF = 20 cm.

b) Đổi 10,8 dm² = 1080 cm².

MN // BC mà AH ⊥ BC nên AK ⊥ MN hay AK là đường cao của tam giác AMN.

Ta có: 

Tương tự, có: 

Nên: S_MNEF = S_ΔAEF – S_ΔAMN = 480 – 120 = 360 (cm²)

Vậy diện tích tứ giác MNFE là 360 cm².