Bài 8.20 trang 57 Toán 6 Tập 2 Kết nối tri thức

Bài 8.20 trang 57 Toán 6 Tập 2 Kết nối tri thức:

Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C.

Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A, B và C.

a) Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho?

b) Tìm trên đường thẳng d điểm G sao cho ba điểm D, E, G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?

Giải bài 8.20 trang 57 Toán 6 Tập 2 Kết nối tri thức:

Ta có hình vẽ sau:

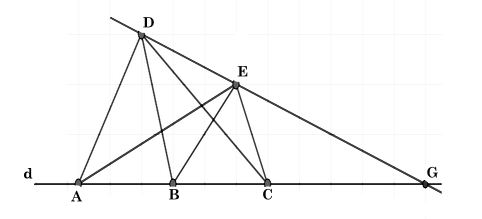
a) Có 8 đường thẳng là: AB (hay BC, AC); AD; AE; BD; BE; CD; CE; DE.

b) Vẽ đường thẳng DE. 

• Nếu đường thẳng DE cắt đường thẳng d tại G thì ba điểm D, E, G thẳng hàng như hình trên

• Nếu đường thẳng DE song song với với d thì không tìm được được G nào thỏa mãn G nằm trên đường thẳng d mà D, E, G thẳng hàng.